Gesetz Der Großen Zahlen Einfach Erklärt
Gesetz der großen zahlen einfach erklärt. Der zentrale Grenzwertsatz beschreibt das Phänomen dass reale zufällige Prozesse in ihrer Summe häufig glockenförmige Verteilungen aufweisen. Gesetz der großen Zahlen Beispiel Würfelwurf. Als Gesetze der großen Zahlen abgekürzt GGZ werden bestimmte Grenzwertsätze der Stochastik bezeichnet.
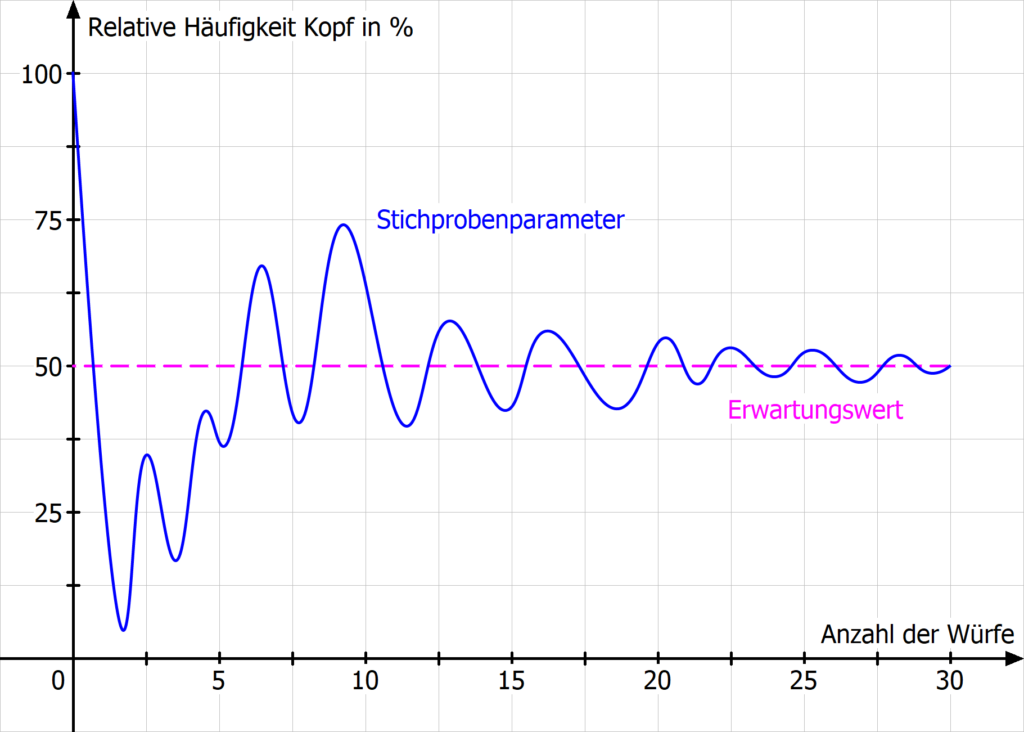
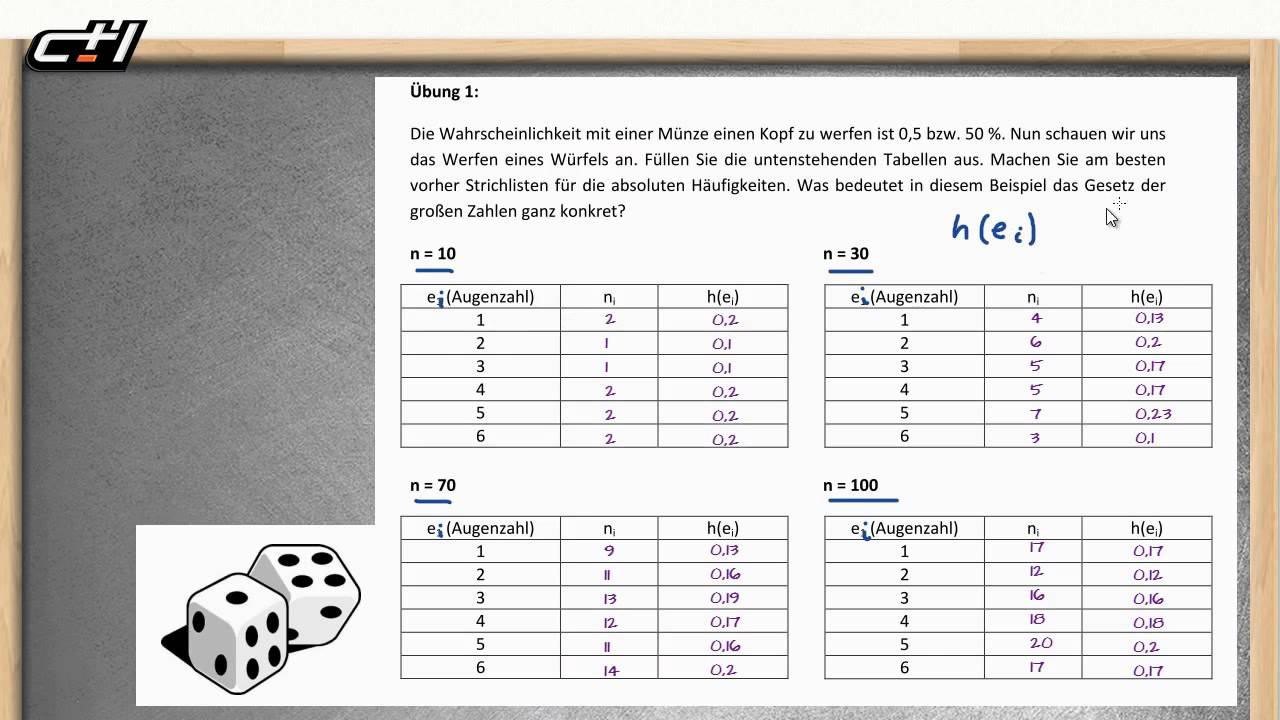
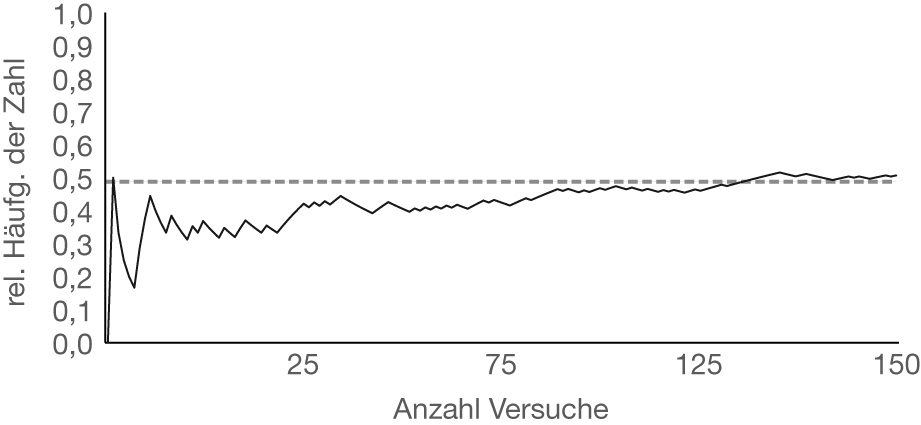
So sind zum Beispiel Wachstumsprozesse wie die Körpergröße aller Männer oder Messvorgänge wie beispielsweise. Das Gesetz der großen Zahlen sagt nun aus dass je häufiger Sie das Zufallsexperiment unter den gleichen Umständen wiederholen desto mehr nähert sich die relative Häufigkeit des Zufallsergebnisses an die Wahrscheinlichkeit an. Ist die Anzahl von Coups genügend groß so entfällt auf jede einzelne Nummer der gleiche Anteil nämlich 137 27.
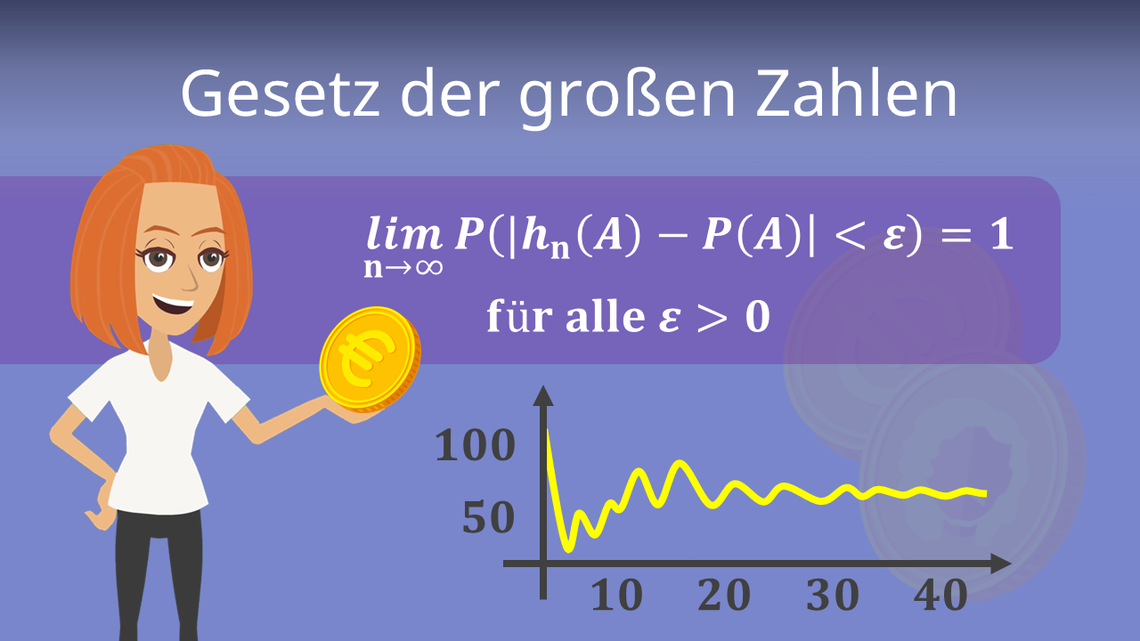
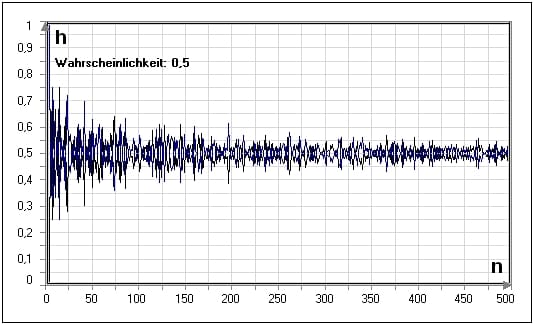
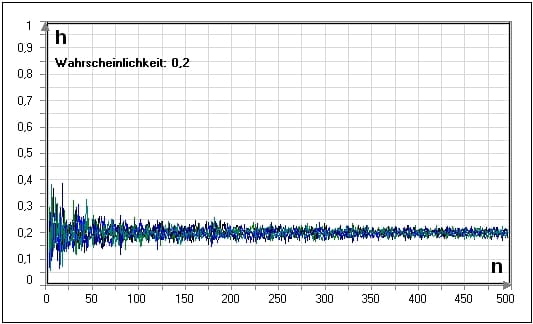
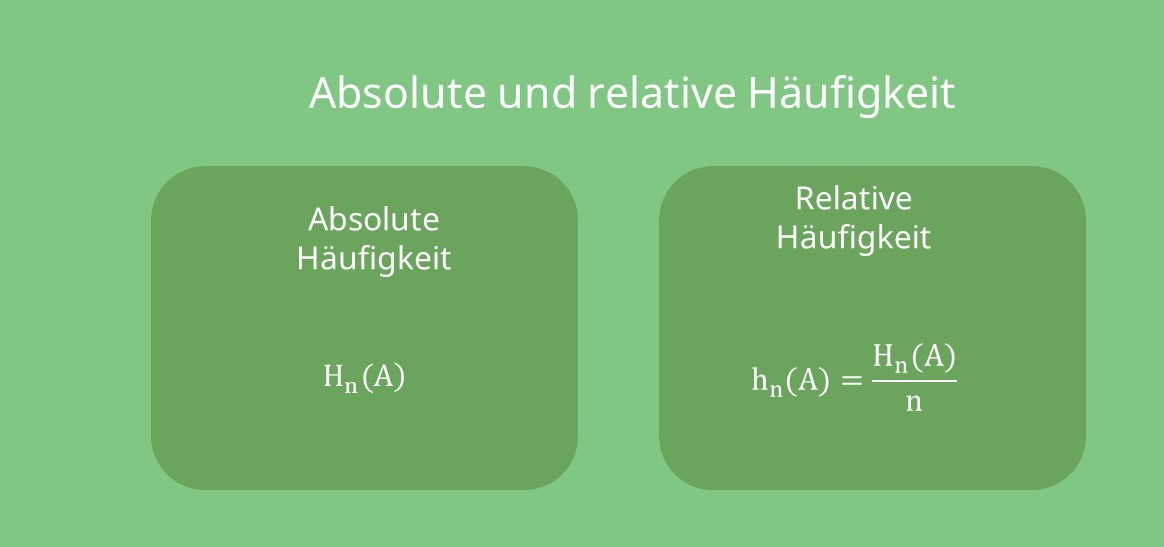
Gesetz der großen Zahlen. Wiederholt man das Experiment bei gleichen Bedingungen n -mal so nähert sich die relative Häufigkeit hn A H A n H A ist die absolute Häufigkeit mit wachsendem n immer mehr der Wahrscheinlichkeit p A des Ereignisses an. Ein Gesetz der großen Zahlen sagt dass mit zunehmender Zahl von Experimentsdurchführungen immer wahrscheinlicher wird dass die ermittelte relative Häufigkeit sich dem echten Wahrscheinlichkeitswert annähert.
Man sagt eine Folge Xk kℕ von Zufallsgrößen genügt dem schwachen Gesetz der großen Zahlen wenn eine Folge an nℕ reeller Zahlen existiert so daß die Folge Yn an nℕ für n in Wahrscheinlichkeit gegen Null konvergiert Konvergenzarten für Folgen zufälliger Größen d. Unter dem Gesetz der großen Zahl versteht man eine Reihe von Formulierungen deren Kern es ist dass Wahrscheinlichkeitsaussagen desto besser zutreffen je größer eine Stichprobe ist bzw. Gesetz der großen Zahlen Das Gesetz der großen Zahlen besagt dass sich die relative Häufigkeit eines Zufallsergebnisses immer weiter an die theoretische Wahrscheinlichkeit für dieses Ergebnis annähert je häufiger das Zufallsexperiment durchgeführt wird.
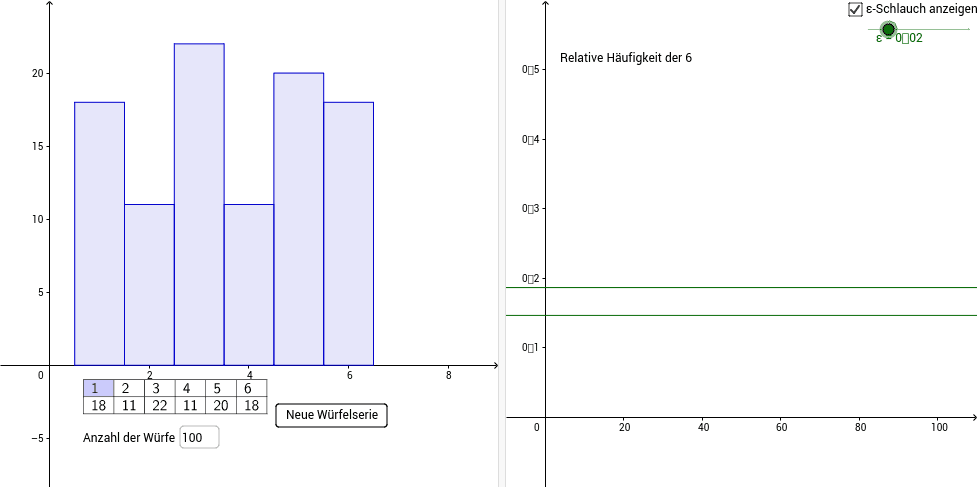
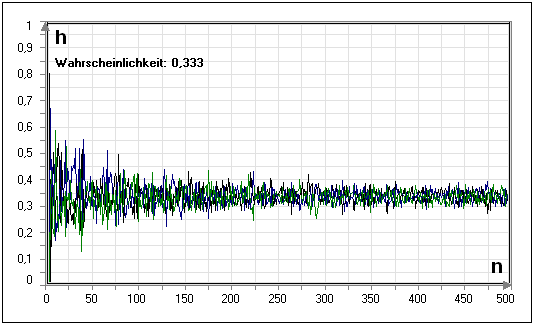
EMPIRISCHES GESETZ DER GROSSEN ZAHL einfach erklärt. Zwischendurch kann sich die relative Häufigkeit natürlich auch wieder weiter von der Wahrscheinlichkeit entfernen wenn Sie im Würfelwurfbeispiel beispielsweise. Nach dem Gesetz der großen Zahlen tritt im langfristigen Mittel jede der 37 Zahlen mit der gleichen relativen Häufigkeit auf d.
Das Gesetz der großen Zahlen theoretisiert dass der Mittelwert einer großen Zahl von Ergebnissen den Erwartungswert genau widerspiegelt und dass der Unterschied abnimmt je mehr Ergebnisse eingeführt werden. EMPIRISCHES GESETZ DER GROSSEN ZAHL einfach erklärt und leicht verständlich aufbereitet - YouTube. Je häufiger ein Zufallsexperiment ausgeführt wird.
Das Gesetz der großen Zahlen. In ihrer einfachsten Form besagen diese Sätze dass sich die relative Häufigkeit eines Zufallsergebnisses in der Regel um die theoretische Wahrscheinlichkeit eines Zufallsergebnisses stabilisiert wenn das zugrundeliegende Zufallsexperiment immer wieder unter denselben.
Ganz einfach ausgedrückt besagt das Gesetz dass je größer eine Stichprobe ist desto wahrscheinlicher stellt sie die echte Wahrscheinlichkeit eines.
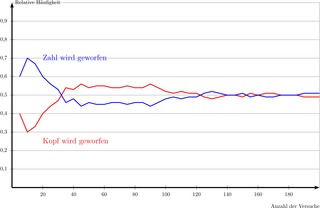
Zwischendurch kann sich die relative Häufigkeit natürlich auch wieder weiter von der Wahrscheinlichkeit entfernen wenn Sie im Würfelwurfbeispiel beispielsweise. Man sagt eine Folge Xk kℕ von Zufallsgrößen genügt dem schwachen Gesetz der großen Zahlen wenn eine Folge an nℕ reeller Zahlen existiert so daß die Folge Yn an nℕ für n in Wahrscheinlichkeit gegen Null konvergiert Konvergenzarten für Folgen zufälliger Größen d. So sind zum Beispiel Wachstumsprozesse wie die Körpergröße aller Männer oder Messvorgänge wie beispielsweise. Als Gesetze der großen Zahlen abgekürzt GGZ werden bestimmte Grenzwertsätze der Stochastik bezeichnet. Nach dem Gesetz der großen Zahlen tritt im langfristigen Mittel jede der 37 Zahlen mit der gleichen relativen Häufigkeit auf d. Gesetz der großen Zahlen Das Gesetz der großen Zahlen besagt dass sich die relative Häufigkeit eines Zufallsergebnisses immer weiter an die theoretische Wahrscheinlichkeit für dieses Ergebnis annähert je häufiger das Zufallsexperiment durchgeführt wird. Wir wissen nun dass beim Münzwurf eine. Das Gesetz der großen Zahlen sagt nun aus dass je häufiger Sie das Zufallsexperiment unter den gleichen Umständen wiederholen desto mehr nähert sich die relative Häufigkeit des Zufallsergebnisses an die Wahrscheinlichkeit an. EMPIRISCHES GESETZ DER GROSSEN ZAHL einfach erklärt.
Das Gesetz der großen Zahlen sagt nun aus dass je häufiger Sie das Zufallsexperiment unter den gleichen Umständen wiederholen desto mehr nähert sich die relative Häufigkeit des Zufallsergebnisses an die Wahrscheinlichkeit an. Als Gesetze der großen Zahlen abgekürzt GGZ werden bestimmte Grenzwertsätze der Stochastik bezeichnet. Wiederholt man das Experiment bei gleichen Bedingungen n -mal so nähert sich die relative Häufigkeit hn A H A n H A ist die absolute Häufigkeit mit wachsendem n immer mehr der Wahrscheinlichkeit p A des Ereignisses an. Das Gesetz der großen Zahlen. Zwischendurch kann sich die relative Häufigkeit natürlich auch wieder weiter von der Wahrscheinlichkeit entfernen wenn Sie im Würfelwurfbeispiel beispielsweise. Begin eqnarray Y_ n- a_ nmathop to limits P0end eqnarray. Gesetz der großen Zahlen Beispiel Würfelwurf Stochastik Wahrscheinlichkeit Mathe by Daniel Jung - YouTube.



























Posting Komentar untuk "Gesetz Der Großen Zahlen Einfach Erklärt"